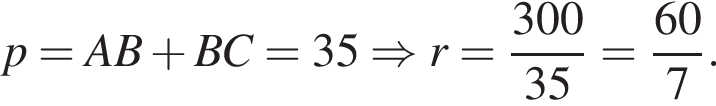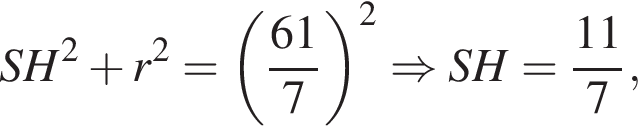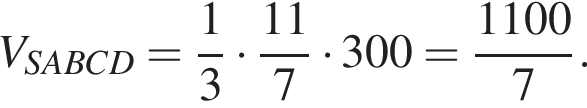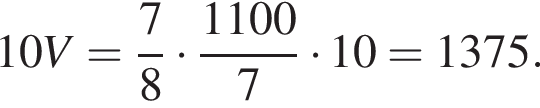Укажите номера прямоугольников, изображенных на рисунках 1−5, при вращении которых вокруг стороны AD получается цилиндр, осевым сечением которого является квадрат.
На клетчатой бумаге с клетками размером 1 см х 1 см изображён параллелограмм. Найдите его площадь в квадратных сантиметрах.
Прямые a и b, пересекаясь, образуют четыре угла. Известно, что сумма трех углов равна 210°. Найдите градусную меру меньшего угла.
Результат разложения многочлена x (4a − b) + b − 4a на множители имеет вид:
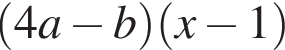
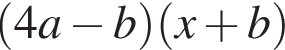
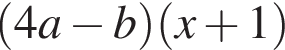
Среди точек С(33), D(24), Е(28), F(43), К(12) координатной прямой укажите точку, симметричную точке А(5) относительно точки В(19).
Найдите значение выражения 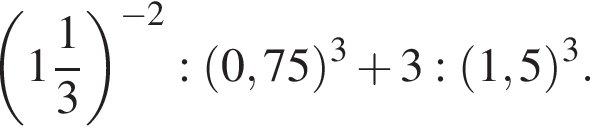
Точка A находится в узле сетки (см.рис).
Если точка B симметрична точке А относительно начала координат, то длина отрезка АВ равна:
Среди данных чисел укажите номера четных чисел, если известно, что число а — нечетное.
| 1) 8 · a; | 2) 11 · a | 3) a + 6 | 4) a2 | 5) a + 13 |
От пристани одновременно отправляются по течению реки катер(I) и против течения реки моторная лодка (II). На рисунке приведены графики их движения. Определите скорость течения реки (в км/ч), если катер и моторная лодка имеют одинаковые собственные скорости.
График уравнения 1,8x − 0,6y = a проходит через точку А(−2; 9). Найдите число a.
Найдите значение выражения 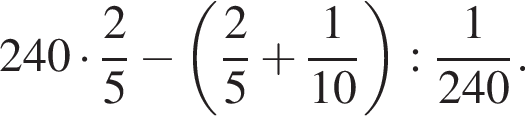
Отрезок AB пересекает плоскость α в точке O. Точка M делит отрезок AB в отношении 3 : 2, считая от точки А. Из точек А, В, M проведены параллельные прямые, пересекающие плоскость α в точках A1, B1, M1 соответственно. Найдите длину отрезка ММ1, если 
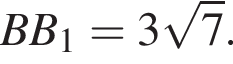
Сократите дробь 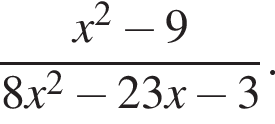
Основанием прямой треугольной призмы ABCA1B1C1 является треугольник АВС, в котором 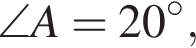
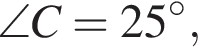 а радиус описанной около него окружности равен
а радиус описанной около него окружности равен ![]() Найдите длину диагонали грани AA1C1C, если площадь этой грани равна
Найдите длину диагонали грани AA1C1C, если площадь этой грани равна ![]()
Найдите сумму всех натуральных чисел n, для которых выполняется равенство НОК(n,63) = 63.
Укажите номера уравнений, которые являются равносильными:
1. 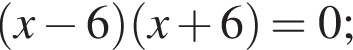
2. 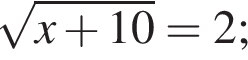
3. 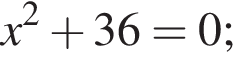
4. 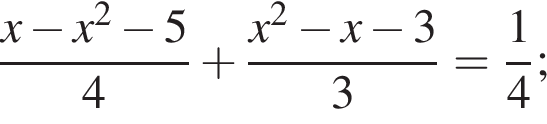
5. 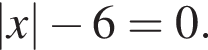
Точки А и В расположены в узлах сетки (см. рис.) и являются соседними вершинами квадрата АВСD. Найдите площадь квадрата ABСD.
Сумма корней (корень, если он единственный) уравнения 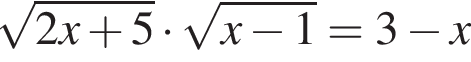 равна (равен):
равна (равен):
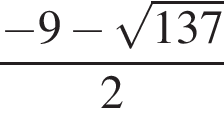
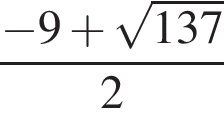
Если в правильной четырехугольной пирамиде высота равна 4, а площадь диагонального сечения равна 12, то ее объем равен ...
Диагонали трапеции равны 15 и 20. Найдите площадь трапеции, если ее средняя линия равна 12,5.
Выберите три верных утверждения, если известно, что две перпендикулярные плоскости
![]() и
и ![]() пересекаются по прямой a и точка A принадлежит плоскости
пересекаются по прямой a и точка A принадлежит плоскости ![]() (см. рис.).
(см. рис.).
1. Любая прямая, проходящая через точку A и пересекающая плоскость ![]() пересекает прямую a.
пересекает прямую a.
2. Существует единственная прямая, проходящая через точку A и перпендикулярная плоскости ![]()
3. Прямая, проходящая через точку A и перпендикулярная плоскости ![]() перпендикулярна плоскости
перпендикулярна плоскости ![]()
4. Любая точка прямой a лежит в плоскостях ![]() и
и ![]()
5. Любая прямая, лежащая в плоскости ![]() и перпендикулярная прямой a, перпендикулярна плоскости
и перпендикулярная прямой a, перпендикулярна плоскости ![]()
6. Любая прямая, перпендикулярная прямой a, принадлежит плоскости ![]()
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 123.
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
Найдите значение выражения 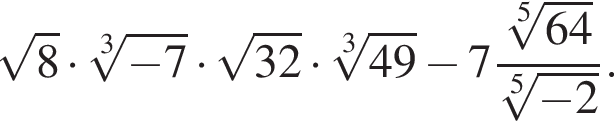
Площадь прямоугольника ABCD равна 20. Точки M, N, P, Q — середины его сторон. Найдите площадь четырехугольника между прямыми AN, BP, CQ, DM.
Функция y = f(x) определена на множестве действительных чисел ![]() является нечетной, периодической с периодом T = 10 и при
является нечетной, периодической с периодом T = 10 и при  задается формулой
задается формулой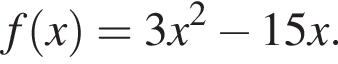 Найдите произведение абсцисс точек пересечения прямой y = 12 и графика функции y = f(x) на промежутке [ −13; 7].
Найдите произведение абсцисс точек пересечения прямой y = 12 и графика функции y = f(x) на промежутке [ −13; 7].
Найдите произведение корней (корень, если он единственный) уравнения 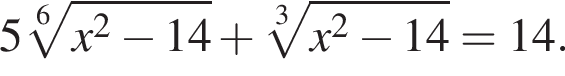
Сфера проходит через все вершины нижнего основания правильной четырехугольной призмы и касается ее верхнего основания. Найдите площадь сферы, если площадь диагонального сечения призмы равна ![]() а высота призмы в два раза меньше радиуса сферы.
а высота призмы в два раза меньше радиуса сферы.
Найдите произведение наибольшего отрицательного и наименьшего положительного целых решений неравенства 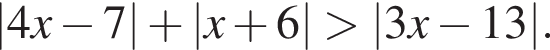
Найдите значение выражения 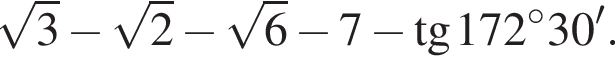
Найдите сумму всех трехзначных чисел, которые при делении на 4 и на 6 дают в остатке 1, а при делении на 9 дают в остатке 4.
Петя записал на доске два различных натуральных числа. Затем он их сложил, перемножил, вычел из большего записанного числа меньшее и разделил большее на меньшее. Сложив четыре полученных результата, Петя получил число 1521. Найдите все такие пары натуральных чисел. В ответ запишите их сумму.
Основанием пирамиды SABCD является выпуклый четырехугольник ABCD, диагонали АС и BD которого перпендикулярны и пересекаются в точке O, АО = 9, ОС = 16, ВО = OD = 12. Вершина S пирамиды SABCD удалена на расстояние ![]() от каждой из прямых AB, BC, СD и AD. Через середину высоты пирамиды SABCD параллельно ее основанию проведена секущая плоскость, которая делит пирамиду на две части. Найдите значение выражения 10 · V, где V — объем большей из частей.
от каждой из прямых AB, BC, СD и AD. Через середину высоты пирамиды SABCD параллельно ее основанию проведена секущая плоскость, которая делит пирамиду на две части. Найдите значение выражения 10 · V, где V — объем большей из частей.

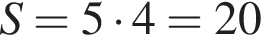 см2.
см2. равна 360°, поэтому четвертый угол равен 150°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 30°.
равна 360°, поэтому четвертый угол равен 150°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 30°.
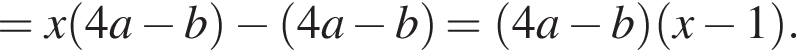

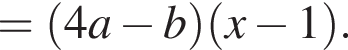
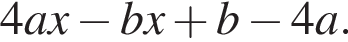
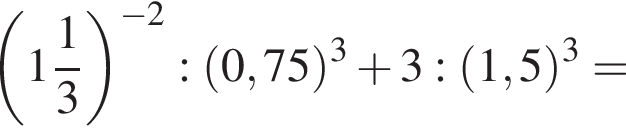

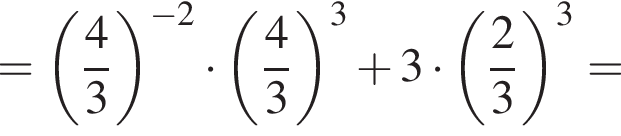
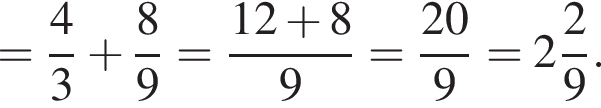
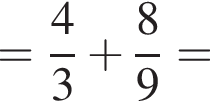
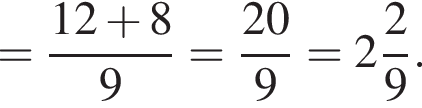
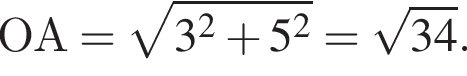
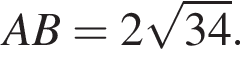
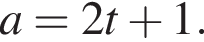 Тогда имеем:
Тогда имеем: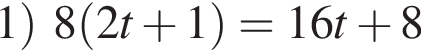 — четное;
— четное;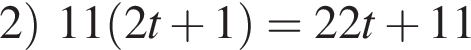 — нечетное;
— нечетное; — нечетное;
— нечетное; — нечетное;
— нечетное;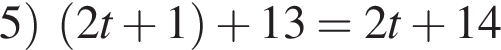 — четное.
— четное.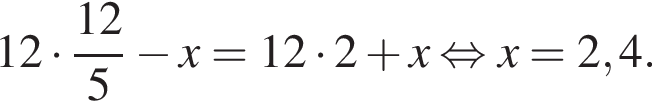
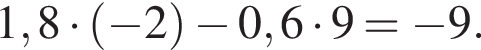
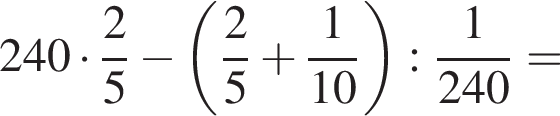
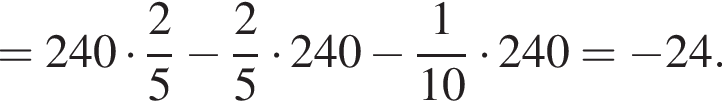
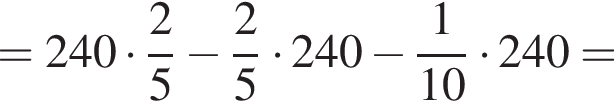
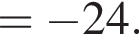
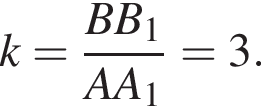 Известно, что
Известно, что 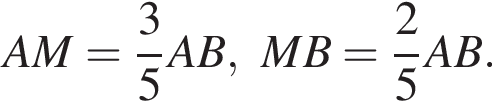 Тогда
Тогда 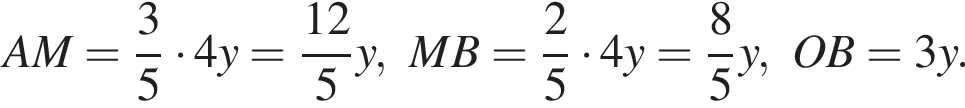
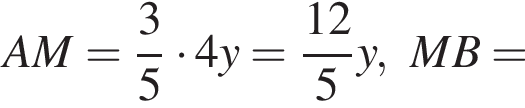
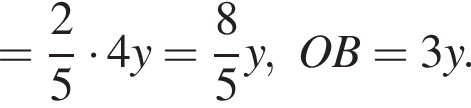
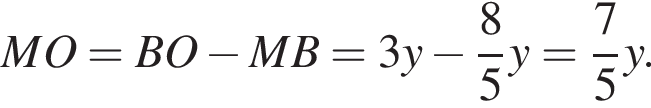 Из подобия треугольников имеем:
Из подобия треугольников имеем: 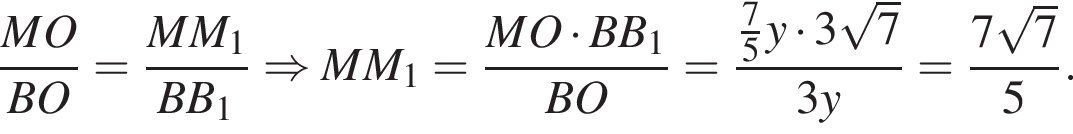
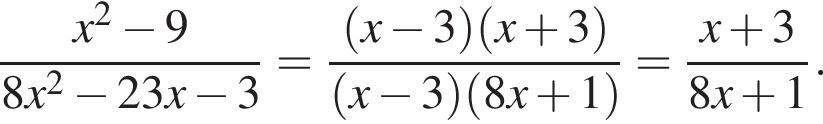
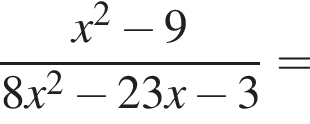
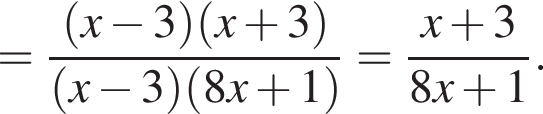
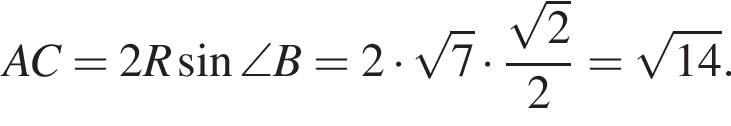
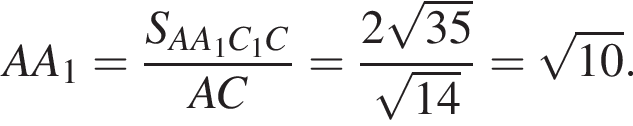
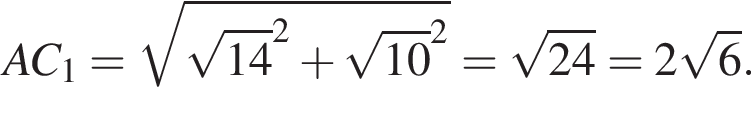
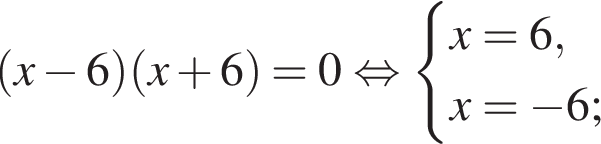
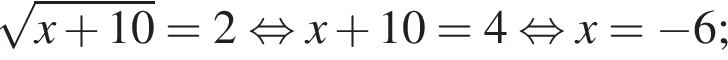
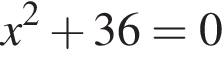 — корней нет;
— корней нет;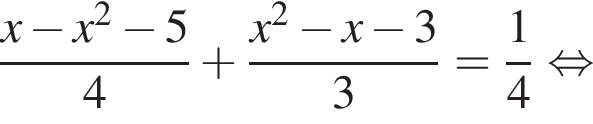
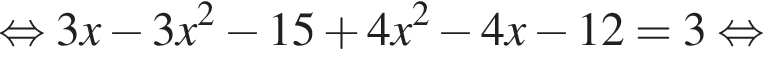
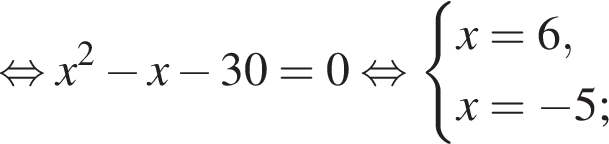
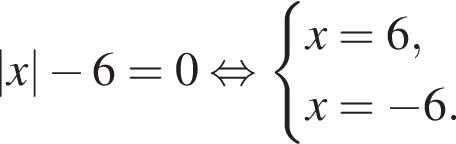
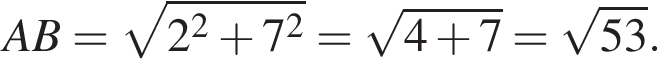

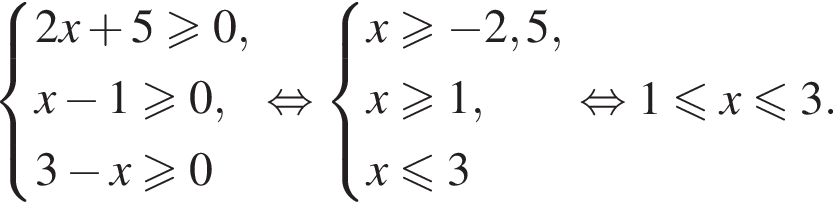
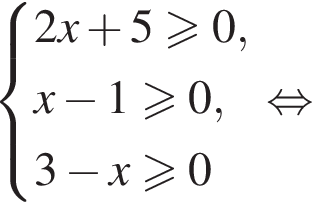
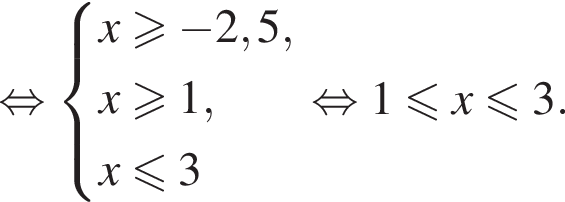
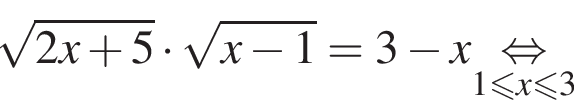
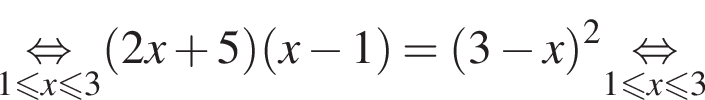
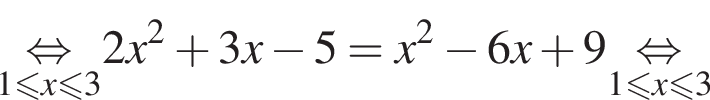
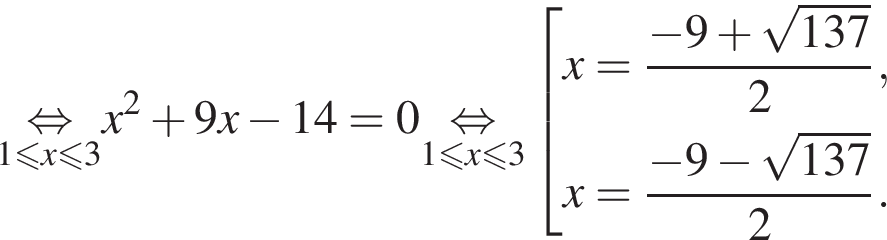
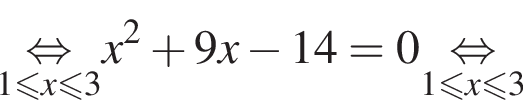
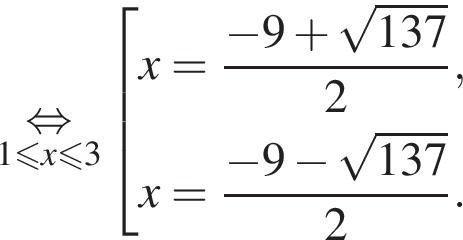
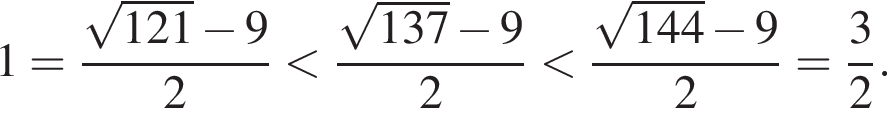
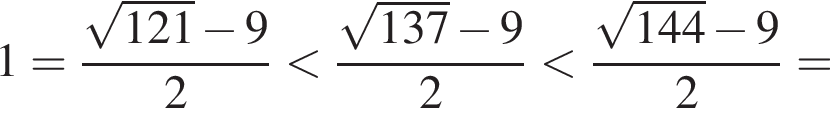
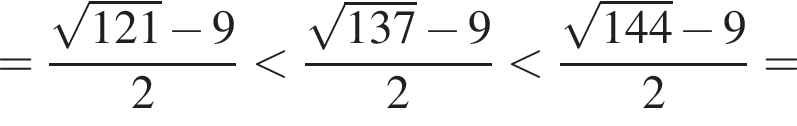
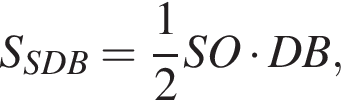 следовательно,
следовательно, 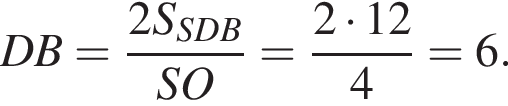
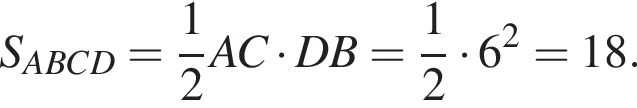 Следовательно,
Следовательно,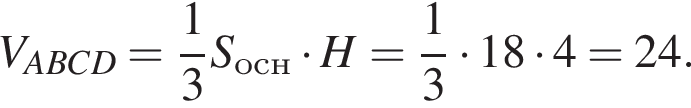
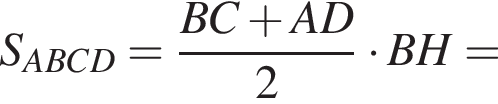
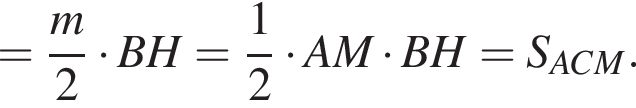
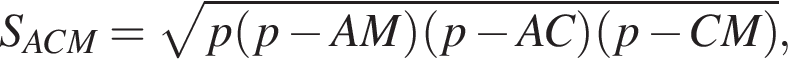 где p — полупериметр треугольника ACM, который равен:
где p — полупериметр треугольника ACM, который равен: 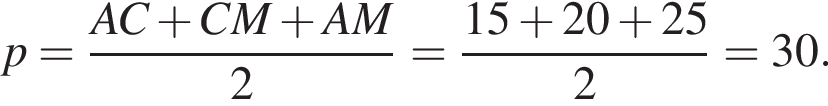

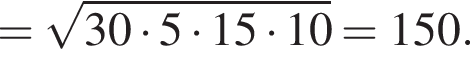
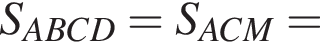

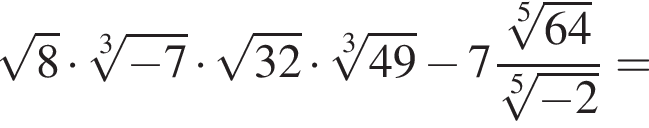
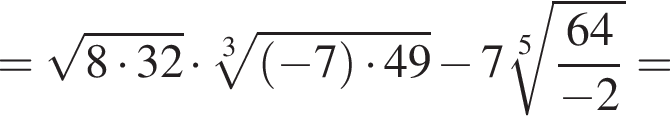
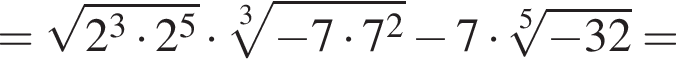
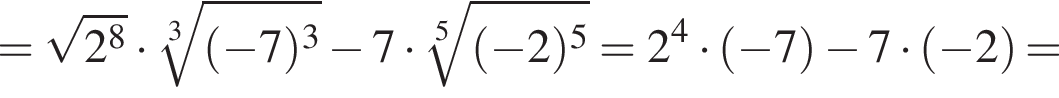
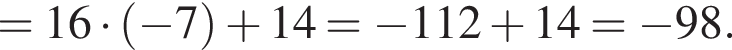
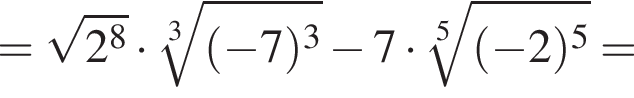
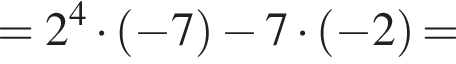
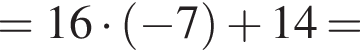

 Поскольку
Поскольку 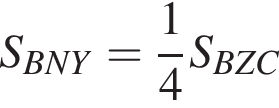 (NY — средняя линия), поэтому
(NY — средняя линия), поэтому 
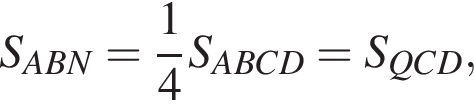 тогда
тогда 

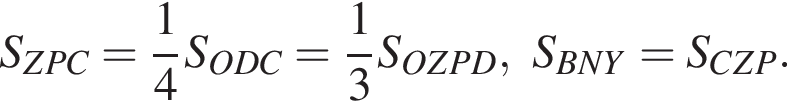
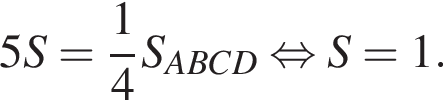
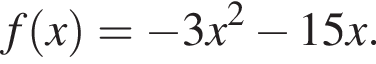 Данный интервал входит в промежуток, на котором необходимо найти произведение абсцисс. Найдем абсциссы точек пересечения полученной функции и прямой y = 12.
Данный интервал входит в промежуток, на котором необходимо найти произведение абсцисс. Найдем абсциссы точек пересечения полученной функции и прямой y = 12. 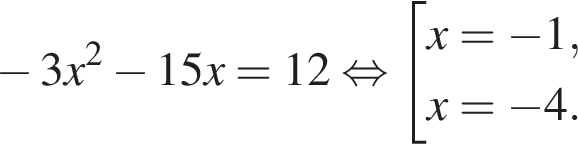
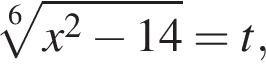
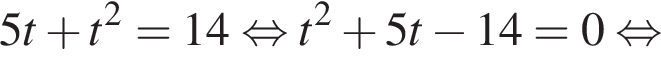
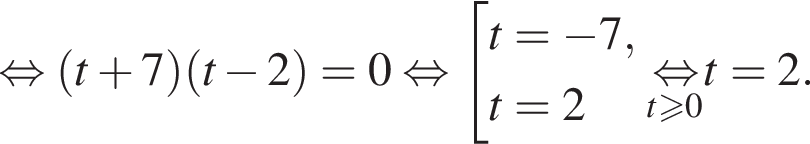
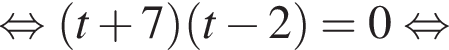
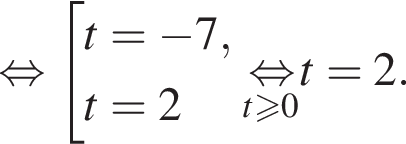
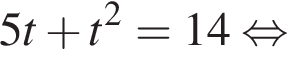
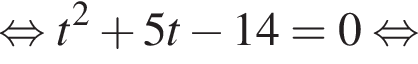
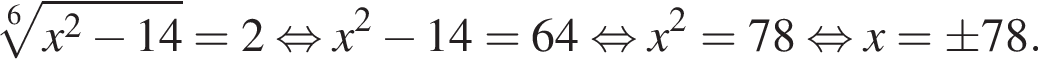
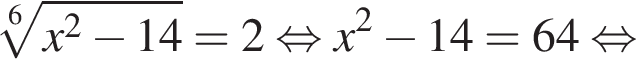

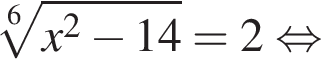
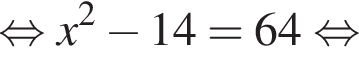

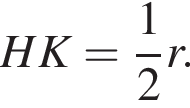 Найдем стороны прямоугольного треугольника AHO:
Найдем стороны прямоугольного треугольника AHO: 
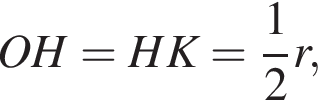 отсюда
отсюда 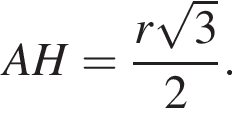 Площадь диагонального сечения
Площадь диагонального сечения 
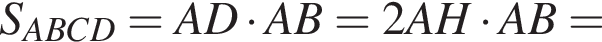
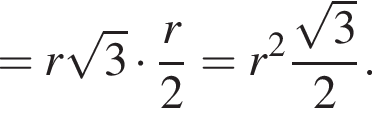
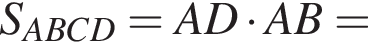
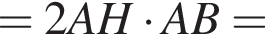
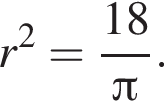 Таком образом,
Таком образом,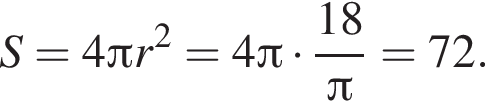
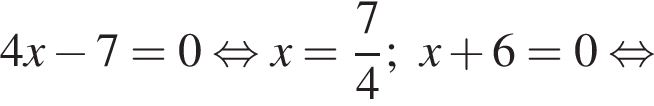
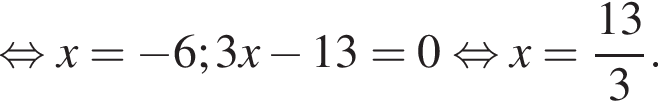
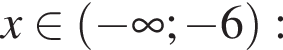
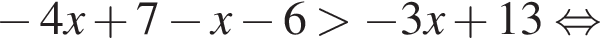

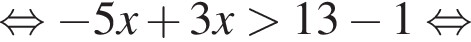
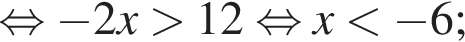
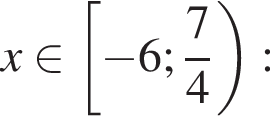




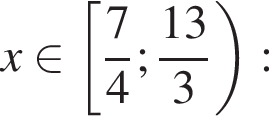
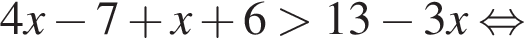
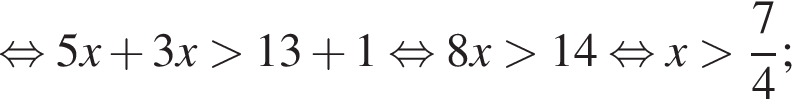

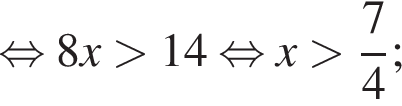
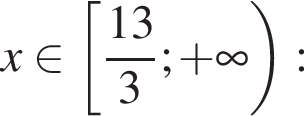

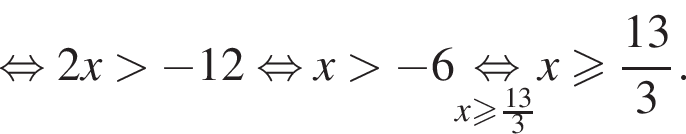
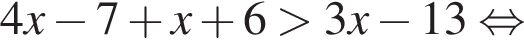

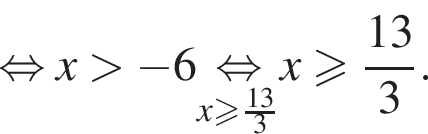


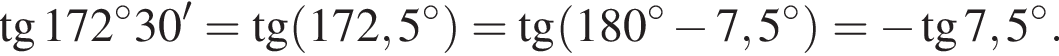
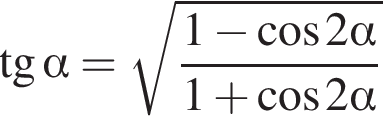 :
: 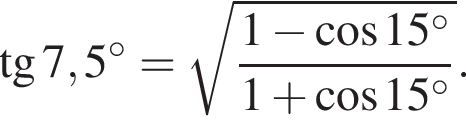



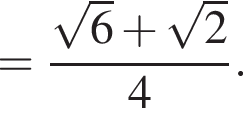
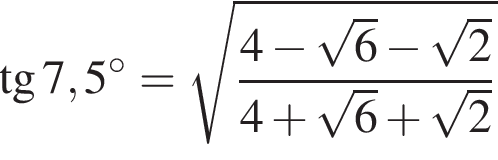
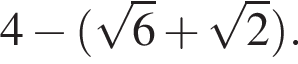 Тогда:
Тогда: 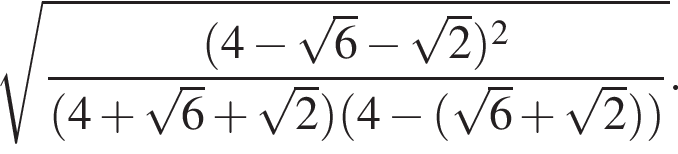
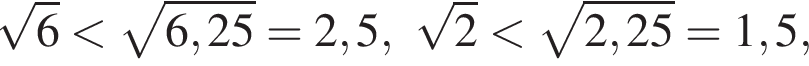
 тогда
тогда 
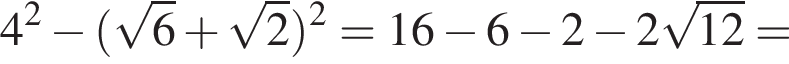

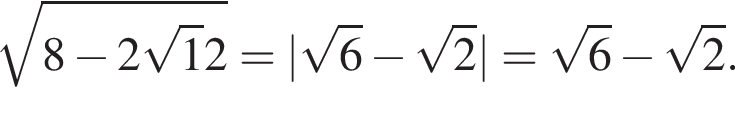 Тогда:
Тогда: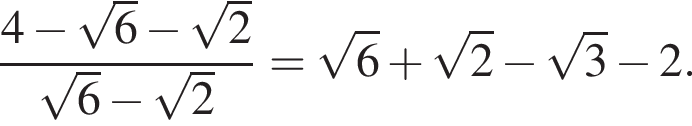
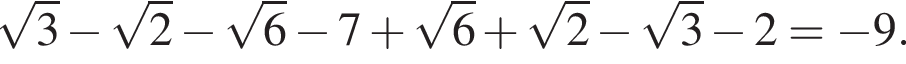
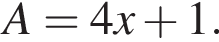


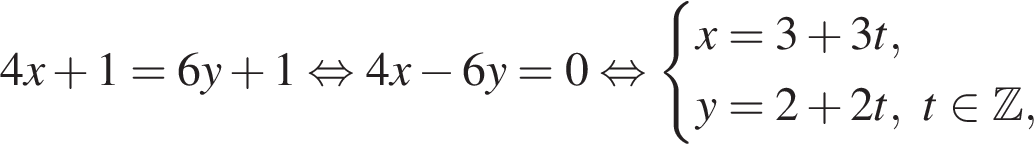
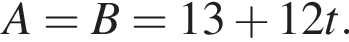
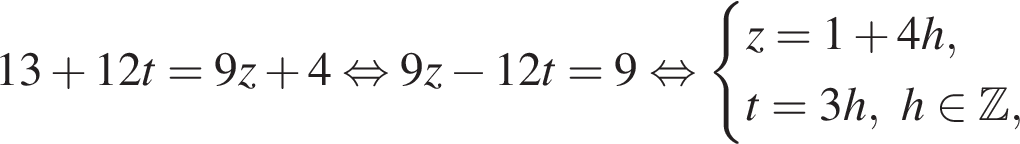

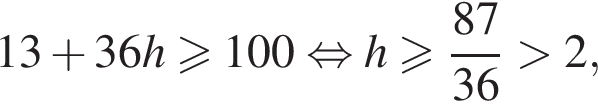 h — целое, поэтому
h — целое, поэтому  h — целое, поэтому
h — целое, поэтому 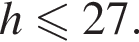
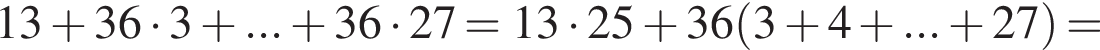
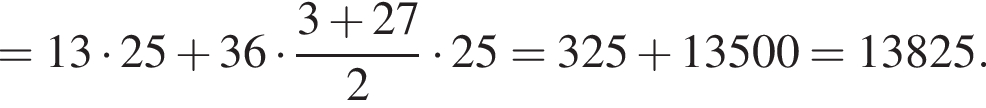
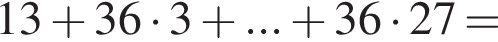
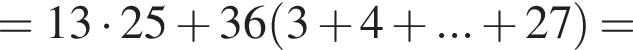
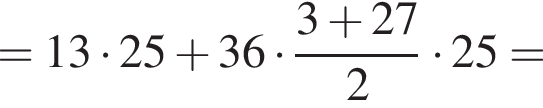

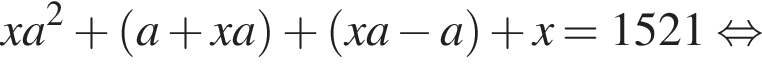
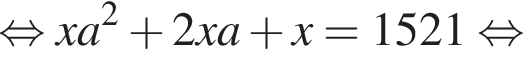

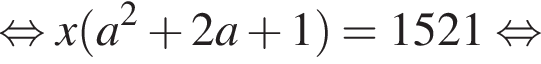
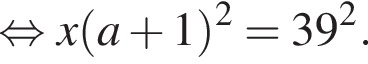
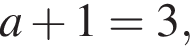
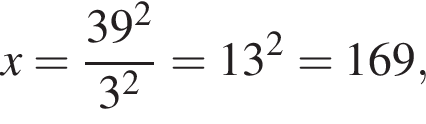
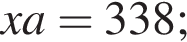
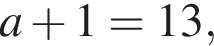
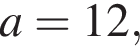
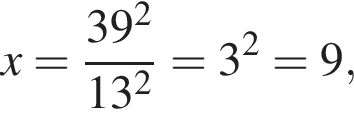
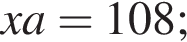
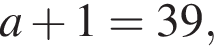
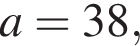
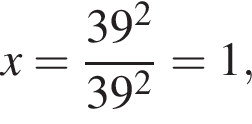
 что запрещено по условию.
что запрещено по условию.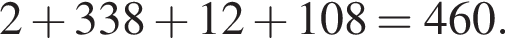
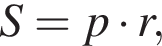 где p — полупериметр. Находим:
где p — полупериметр. Находим: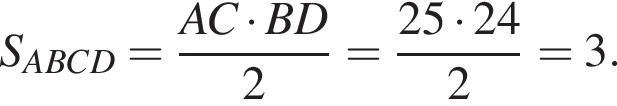
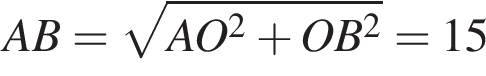 и
и 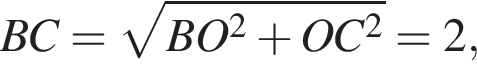 следовательно,
следовательно,